Sprint2_Hypothesis test

 

 

어제 배웠던 T-test에 보충 설명이다.

 

T-test를 하기 위해서는 몇 가지 조건이 따른다.

 

1. 독립성 : 두 그룹이 서로 독립적 이어야 한다.

  - 독립적이라는 의미는 비교하려는 두 집단의 구성이 서로 관계가 없어야 한다는 것을 의미한다.

 

2. 정규성 : 데이터가 특정 값에 편향되지 않고 적절히 잘 수집 되었는지 확인해야 한다.

 

3. 등분산성 : 두 그룹의 분산이 어느 정도 유사한지 확인해야 한다.

 

normaltest(data)

python에서는 nomaltest()를 통해 등분산성을 파악할 수 있다.

 

 

키, 몸무게와 같은 연속형 자료(수량화 할 수 있는 데이터)를 분석할 때에는 T-test와 ANOVA 분석 방법이 사용된다.

 

반면에, 성별, 혈액형 등 범주형 자료(수량화 할 수 없는 데이터)를 분석할 때는 카이제곱검정법이 사용된다.

 

 

Chi-squared test (카이제곱검정)

 

데이터의 분포가 균등한가를 검증하기 위해 비교하는 것으로 categorical data에서 사용 가능하다. t-test와 마찬가지로 one sample 카이제곱, two sample 카이제곱이 존재한다.

 

 

1) One-sample Chi-squared

 

One-sample 카이제곱은 "내가 가진 주사위가 동일한 빈도를 나타내는가"로 예를 들 수 있다.

만약 내가 주사위를 120번 던진다고 가정하면, 1~6이 20번씩 나온다고 예상할 수 있다.

 

여기서 20번이라는 숫자는 기대값이라하고, 실제로 던져서 나온 값은 관측값이다.

 

One-sample chi-squared의 귀무가설은 다음과 같다.

 

H0 : 관측값과 기대값이 동일하다.

H1 : 관측값과 기대값이 다르다.

 

카이제곱도 t-test와 같이 scipy라이브러리를 사용하여 검정할 수 있다.

python에서 one-sample chi-squared를 구하는 코드는 아래와 같다.

from scipy.stats import chisquare

chisquare(data, axis=None)

 

p-value가 0.05보다 크면 귀무가설을 기각할 수 없다. 따라서 관측값과 기대값이 동일하다.

 

2) Two-sample Chi-squared

 

Two-sample 카이제곱은 두 표본집단의 분포가 동일한지 확인할 때 사용한다. (상관관계)

 

Two-sample chi-squared의 귀무가설은 다음과 같다.

 

H0 : A와 B는 서로 연관성이 없다. (=독립이다.)

H1 : A와 B는 서로 연관성이 있다.(=독립이 아니다.)

 

python에서 two-sample chi-squared를 구하는 코드는 아래와 같다.

from scipy.stats import chi2_contingency

chi2_contingency(data1, correction=False)

 

p-value가 0.05보다 작으면 귀무가설을 기각하고 대립가설을 채택한다. 따라서 두 데이터는 서로 연관성이 있다.

 

 

One-tailed vs Two-tailed

 

어제 이 부분이 이해가 안갔는데 이제 좀 알 것 같다.

 

 

1) Two-tailed

 

가설이 아래와 같다고 가정한다.

 

H0 : 모집단의 평균이 A와 같다.

H1 : 모집단의 평균이 A와 다르다.

 

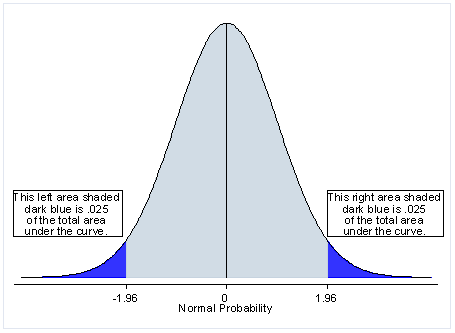
0.05의 유의 수준을 사용할 경우 Two-tailed는 값을 반으로 나누어 양 쪽 꼬리에 각각 0.25의 기각력을 가진다.

즉, 내가 뽑은 표본이 2.5%내에 들면 귀무가설을 기각할 수 있다. 

 

https://stats.idre.ucla.edu/other/mult-pkg/faq/general/faq-what-are-the-differences-between-one-tailed-and-two-tailed-tests/

 

2) One-tailed

 

One-tailed의 가설은 아래와 같이 가정한다.

 

H0 : 모집단의 평균이 A와 같다.

H1 : 모집단의 평균이 A보다 작다. or 크다.

 

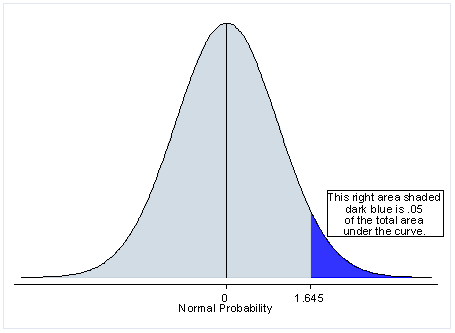
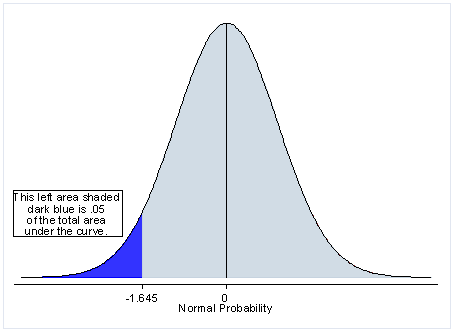
One-tailed는 관심있는 한 방향의 통계적 유의수준을 모두 할당한다.

만약 H1을 모집단의 평균이 A보다 크다라고 가정하면, 오른쪽에만 기각력이 0.05 위치한다.

 

 

https://stats.idre.ucla.edu/other/mult-pkg/faq/general/faq-what-are-the-differences-between-one-tailed-and-two-tailed-tests/

 

 

Reference

velog.io/@gayeon/%EB%8D%B0%EC%9D%B4%ED%84%B0-%EB%B6%84%EC%84%9D-%EC%B4%88%EB%B3%B4%EC%9E%90%EB%A5%BC-%EC%9C%84%ED%95%9C-T-test-Chi-squared-test

hsm-edu.tistory.com/146

https://stats.idre.ucla.edu/other/mult-pkg/faq/general/faq-what-are-the-differences-between-one-tailed-and-two-tailed-tests/